베르누이 분포
- 베르누이 시행 : 결과가 두 가지 중 하나로만 나오는 시행
- 베르누이 확률변수 : 베르누이 시행의 결과를 실수 0 또는 1로 바꾼 것
- 1이 나올 확률 $\mu$가 parameter
- 베르누의 확률분포 : 베르누이 확률변수의 분포
- $Bern(x;\mu)=\mu^x(1-\mu)^{1-x}$
이항분포
- 성공 확률이 $\mu$인 베르누이 시행을 $N$번 반복할 때, 성공 횟수
- $Bin(x;N,\mu)={N \choose x}\mu^x(1-\mu)^{1-x}$
카테고리 분포
- 베르누이 분포의 확장판
- 다중 분류에 사용됨
- 각각의 항목이 확률값($\mu_i$)을 가짐
- 즉, $\sum_{i=1}^{K}\mu_i=1$
- $Cat(\boldsymbol{x};\boldsymbol{\mu})=Cat(x_1,x_2,...,x_K;\mu_1,\mu_2,...,\mu_K)=\prod_{k=k}^{K}\mu_{k}^{x_k}$
다항분포
- 이항분포의 확장판
- ex. 주사위를 $N$번 던져 각 면이 나오는 횟수 집합의 분포
- $Mu(x;N,\mu)={N \choose x_1,...x_k}\prod_{k=1}^{K}\mu_{k}^{x_k}$
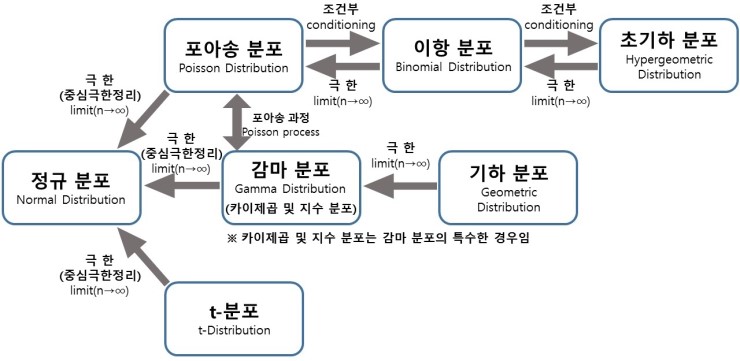
감마분포
- 지수 분포는 첫 번째 사건이 발생할 때 까지 걸린 시간에 대한 분포였다.
- 감마 분포는 $n$ 번째 사건이 발생할 때 까지 걸린 시간에 대한 분포다.
- 즉, 지수 분포는 감마 분포에 $n=1$을 대입한 특수한 경우이다.
- 신뢰성 공학 등에서 고장을 묘사할 때 사용한다.
- $a$는 발생 횟수, $b$는 1회 발생 간격이다.
정규분포
- 연속 확률 분포 중 대표적
- 통계적 추론에서 매우 중요하게 취급됨
- 잡음(noise)을 모델링하거나, 자연적으로 발생하는 현상을 모델링할 때 사용
- 정규분포를 그대로 사용하려니 적분 등의 연산이 복잡하여 보통은 표준정규분포로 만들어 사용한다.
중심극한정리
- 모집단의 분포를 모르더라도 표본의 크기가 충분히 크다면 표본 평균들의 분포가 정규 분포를 따른다.
- 표본 평균들이 이루는 표본 분포와 모집단 간의 관계를 증명함으로써, 수집한 표본의 통계량(statistics)을 이용해 모수(parameters)를 추정할 수 있는 수학적 근거를 마련
카이제곱분포
- 정규분포를 제곱하거나, 정규분포를 제곱한 것을 더한 것을 카이제곱분포라고 한다.
- 제곱해서 더한 것이므로 0보다 큰 영역에서만 그려진다.
- 감마분포의 특수한 형태($X\sim Gamma(a=r/2, b=2) \Leftrightarrow \chi^2(r)$)
- 왼쪽으로 치우치고, 오른쪽으로 긴 꼬리를 갖는 분포
- 자유도 $n$이 커질수록 종모양의 분포에 가까워진다. 즉, $n$이 커질수록 카이제곱분포는 정규분포에 근사한다.
- $X$가 $\chi^2(n_1)$을 따르고, $Y$가 $\chi^2(n_2)$를 따르고, $X$, $Y$가 서로 독립이라면 $X+Y=\chi^2(n_1+n_2)$가 된다. 이를 "$\chi^2$분포의 가법성"이라고 한다.
활용
- 표본분산 $s^2$의 분포
- 범주형 자료 분석의 카이제곱 검정
t 분포
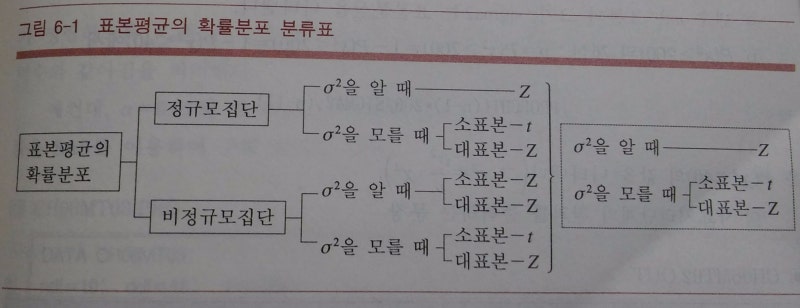
- 정규분포의 한계를 극복하기 위해 개발됨
- 정규분포는 표본의 수가 적으면 신뢰도가 낮아진다. 정규분포보다 한 단계 예측범위가 넓은 분포를 사용하는데, 이것이 t분포이다.
- 공식 외울 필요 없다.
- t 분포의 확률밀도함수는 표준정규분포와 비슷하게 종 모양의 분포를 이루며, t=0에 대해 좌우 대칭이다.
- 다만, t 분포의 꼬리 부분은 표준정규분포보다 약간 더 두터우며(팻 테일), 이는 자유도 $r$이 커질수록 표준정규분포에 가까워진다.
활용
- 평균에 대한 검정이나 추정을 할 때 많이 쓰임
F-분포
- 카이제곱 분포는 한 집단의 분산을 다룸
- F-분포는 두 집단의 분산을 다룸
- 두 집단의 분산의 비율을 통해 분산의 크기를 비교한다.
- 비율이 1에 가까울수록 두 분산의 크기가 비슷한 것이며, 1에서 멀어질수록 두 분산의 크기가 다른 것이다.
- 각각의 카이제곱분포는 자유도를 가지고 있으므로 이들이 F-분포의 자유도가 된다.
- 공식 외울 필요 없다.
- 일반적으로 왼쪽으로 치우친 모양을 가지고 있다.
활용
- 분산에 대한 검정이나 추정을 할 때 많이 쓰임
- 또한, 세 개 이상의 평균 집단의 차이를 검정할 때도 쓰임
베타 분포
- 정규 분포는 $(-\infty, \infty)$에 대해 정의할 수 있지만 베타 분포는 $(0, 1)$에 대해 정의할 수 있다.
- 통계에서 이와 동일한 특성을 갖는 것이 확률이다. 따라서 어떠한 확률을 모델링하기 위한 수단으로 사용할 수 있다.
- $\alpha$, $\beta$를 parameter로 갖는다. 이들이 베타 분포의 모양을 결정한다고 해서 형상인자(shape factor)라고 부르기도 한다.($\alpha>0$, $\beta>0$)
- 베타 분포의 앞에 붙은 것들은 PDF의 적분값이 1이 되도록 만들어주기 위한 상수로, 베타 함수(beta function)이라고 한다.
출처
'스터디' 카테고리의 다른 글
| 02 Fundamentals of Machine Learning (0) | 2020.08.07 |
|---|---|
| 01 Motivations and Basics (0) | 2020.08.07 |
| 6. 피지엠파이(pgmpy)로 공부하는 확률론: 베이즈 정리 (0) | 2020.04.28 |
| 4. 심파이(SymPy)로 공부하는 미적분 (0) | 2020.04.14 |
| 3-4. 고급 선형대수: SVD(1) (0) | 2020.03.30 |