1.2.0. 확률의 법칙
1. 합의 법칙
두사건 A,B가 동시에 일어나지 않을때,
A사건 일어나는 경우의 수가 m, B사건이 일어나는 경우의 수n
m+n
2. 곱의 법칙
두사건 A,B가 동시에 일어날 떄,
A사건 일어나는 경우의 수가 m, B사건이 일어나는 경우의 수n
m*n3. 베이즈정리
- 단하게 이와 관련된 수식을 정리해본다.


- 이 때 ci=∑_jnijci=∑jnij 이다. 이로부터 합의 법칙을 유도할 수 있다.

- 곱의 법칙도 간단하다.
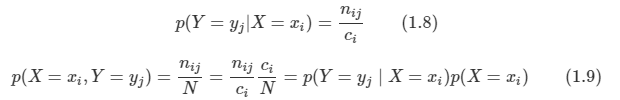
1.2.1. 확률 밀도 (Probabilty densities)
연속적인 변수에서 그변수의 확율이 주어지면 P(x)를 확률 밀도라고 부른다.
확률 값을 구간(range)으로 표현한다. : R(x,x+δx), 여기서 δxδx 가 0에 수렴한다면, 값은 p(x)p(x) 가 된다.

누적분포함수 (CDF)
X가 (- ∞ ,z)범위에 속할때 누적분포함수

cf)콜모고로포
(1) 모든 확률은 0 이상이다.

(2) 표본공간 S가 가능한 모든 전체집합에 대한 확률은 1이다.

(3) 서로 상호배반인 사건 A, B, …에 대해 교집합이 공집합인 사건(부분집합)의 합집합인 사건의 확률은 각 사건(부분집합)의 확률의 합이다.

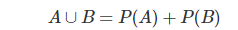
동시에 일어날리 없는 두 사건 중 적어도 하나(합집합의 개념이죠)가 일어날 사건은 두 사건이 일어날 확률은 더한 게 된다
연속 확률 밀도(PDF)
연속적인 확률 밀도에서 p(x)p(x) 를 통해 얻어진 실수 값은 실제 확률 값이 아니라 확률 함수의 반환 값이다.
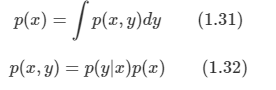
1.2.2. 평균과 공분산 (Expactations and covariances)
각 확률변수들이 어떻게 퍼져있는지를 나타내는 것이 공분산(Covariance)이다.,
두 확률변수 X와 Y가 어떤 모양으로 퍼져있는지
즉, X가 커지면 Y도 커지거나 혹은 작아지거나 아니면 별 상관 없거나 등을 나타내어 주는 것이다.

Cov(X, Y) > 0 X가 증가 할 때 Y도 증가한다.
Cov(X, Y) < 0 X가 증가 할 때 Y는 감소한다.
Cov(X, Y) = 0 공분산이 0이라면 두 변수간에는 아무런 선형관계가 없으며 두 변수는 서로 독립적인 관계에 있음을 알 수 있다.
그러나 두 변수가 독립적이라면 공분산은 0이 되지만, 공분산이 0이라고 해서 항상 독립적이라고 할 수 없다.
확률변수 X의 평균(기대값), Y의 평균을 각각

이라 했을 때, X,Y의 공분산은 아래와 같다.

즉, 공분산은 X의 편차와 Y의 편차를 곱한것의 평균이라는 뜻이다.
좀더 간편하게 정리하면 아래와 같다.


만약에 X와 Y가 독립이면

이므로 공분산은 0이 된다. 그런데 공분산에도 문제점이 하나 있다.
X와 Y의 단위의 크기에 영향을 받는다는 것이다.
확률변수의 절대적 크기에 영향을 받지 않도록 단위화 시켰다고 생각하면 된다.
즉, 분산의 크기만큼 나누었다고 생각하면 된다.
상관계수의 정의는 아래와 같다.

1. 상관계수의 절대값은 1을 넘을 수 없다.
2. 확률변수 X, Y가 독립이라면 상관계수는 0이다.
3. X와 Y가 선형적 관계라면 상관계수는 1 혹은 -1이다.
양의 선형관계면 1, 음의 선형관계면 -1
이상 참고 끝.
- 함수 결과에 대한 평균 값을 설명한다. (각각 이산, 연속 확률 함수이다.)

- 연속 함수에 대한 평균값을 근사하는 방법이 있는데, 최대한 많은 샘플을 생성해서 샘플을 통해 평균을 구하는 방법이 있다.

연속 함수에 대한 평균값을 근사하는 방법이 있는데, 최대한 많은 샘플을 생성해서 샘플을 통해 평균을 구하는 방법이 있다.\

- 이 때 N→∞N→∞ 이면 이 근사 값은 실제 값과 거의 같아지게 된다.
- 그리고 위와 같은 식이 쓸데없이 자꾸 언급되는 이유는 이후에 연속 확률 함수에 대한 샘플링 기법을 소개하기 위함이다.
- 이것도 뒤에 자세히 나오니 그냥 간단하게 확인만 하고 넘어가자.
- 간혹 여러 개의 변수를 사용하는 함수에 대해 평균 값을 표기할 경우가 있다.
- 이 때에는 평균에 사용하는 주변수를 함께 기술한다.

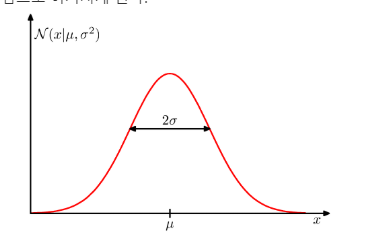
1.2.4. 가우시안 분포 (Gaussian distribution)

이 확률 분포는 2개의 파라미터(모수, parameter)가 존재한다.
- μ : 평균(mean)
- σ : 표준편차(standard deviation)
또한 표준 편차 제곱(즉, 분산)의 역수 β=1/σ2β=1/σ2 를 정확도(precision)라고 정의한다.
- 보통 수식 전개상 분산보다는 정확도를 기준으로 계산하는 것이 더 편리한 경우가 많기 때문.
- 이 교재에서도 수식을 전개할 때 정확도를 더 많이 사용한다.
- 하지만 어차피 분산과 같은 개념으로 여겨지게 된다.
가우시안 분포를 정규 분포라고 부른다. 이 분포는 다음과 같은 성질이 있다.


간결



